Ruled Laguerre minimal surfaces

M. Skopenkov, H. Pottmann and P. Grohs

Abstract:

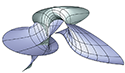
A Laguerre minimal surface is an immersed surface in R³ being an extremal of the functional ∫(H²/K - 1) dA. In the present paper, we prove that the only ruled Laguerre minimal surfaces are the surfaces
      R(φ, λ) = (Aφ, Bφ, Cφ + D cos 2φ) + λ (sinφ, cosφ, 0),
where A, B, C, D ∈ R are fixed. To achieve invariance under Laguerre transformations, we also derive all Laguerre minimal surfaces that are enveloped by a family of cones. The methodology is based on the isotropic model of Laguerre geometry. In this model a Laguerre minimal surface enveloped by a family of cones corresponds to a graph of a biharmonic function carrying a family of isotropic circles. We classify such functions by showing that the top view of the family of circles is a pencil.

Bibtex:

@article{skopenkov-2012-rlms,
    AUTHOR = {Skopenkov, Mikhail and Pottmann, Helmut and Grohs, Philipp},
     TITLE = {Ruled {L}aguerre minimal surfaces},
   JOURNAL = {Math. Z.},
    VOLUME = {272},
      YEAR = {2012},
     PAGES = {645--674},
}

PDF